TECH BLOG
P値の収束に関する数学的考察
CADの西村と石橋です。この記事では、数理統計のトピックの中でも、仮説検定における
みなさんは、「サンプルサイズが大きければ、統計的仮説検定において有意差を検出しやすい」といった議論を目にしたことはありますでしょうか?例えば統計ライブラリー サンプルサイズの決め方 |朝倉書店 (asakura.co.jp)のまえがきや、統計的有意性と P 値に関する ASA 声明などで言及されています。
この現象は数学的にどのように説明できるか?と疑問を持ったのですが、枠組みの定式化において苦労する点が多く、「記事にすれば興味をもっていただけるのでは?」と思い至りました。
なのでこの記事では、「対立仮説が正しい場合、サンプルサイズが大きくなれば
※帰無仮説が正しい場合、
![]() 前提条件
前提条件
まずは、問題の定式化に必要な前提条件を述べようと思います。今回は「分散が既知で、対立仮説の方が正しい」場合の仮説検定を想定します。
標本は分散が存在し平均値で特徴づけられるとある分布
・
・下記の両側検定を考える:
・
・対立仮説
・対立仮説が正しい
目標
証明したいことは以下の形で定式化することができます。
「前提条件の下で, この検定に関する
ちなみに、母集団として正規分布を仮定した場合は
定義
さて、 ”目標”の中で
定義(
最初に統計量
さらに帰無仮説のもとでの
以上の準備の下で、 この検定における
すなわち標本空間の元
ここで注意として、
Amazon.co.jp: 新装改訂版 現代数理統計学 : 竹村 彰通: 本
定義(概収束)
最後に
また、このとき
証明の道具
概収束とは何かわかったところで証明に入っていきたいのですが、 その前に道具を2つ準備しておきます。
大数の強法則
中心極限定理
ここで
Remark.
中心極限定理は法則収束(分布関数列の各点収束)で記述されるのが一般的ですが、 法則収束から分布の一様収束を示すのは容易です。証明はAppendixに記載します。
目標の証明
以上で準備ができたので、目標の主張を証明していきます。
まず、大数の強法則より,
ここで、対立仮説が正しいという仮定から
このとき、
したがって、 中心極限定理と分布関数の基本的な性質から
Appendix
補題
このとき、
補題の証明
ある
また、有界閉区間上の連続関数は一様連続であるため、
ゆえに,
このとき、 任意の
以上から
となり、両辺の上極限を考えれば結論が得られる。
シュミレーション
ここまでの議論で、サンプルサイズ
設定
・母集団分布は一様分布を想定する※
・母平均
・帰無仮説
・対立仮説
この設定で、サンプル数
※分散既知という仮定から、分散から平均値が算出可能な分布を避けるため、一様分布を採用しています。
可視化方法
1. 母集団分布からn個の標本をランダムにサンプリングする
2. 標本平均が正規分布に従っているという仮定の下、
3.
可視化結果
母集団として、以下の3パターンので実験した結果を表示します
・一様分布A:[-1, 1]上の一様分布(平均0、分散1/3:帰無仮説が正しい)
・一様分布B:[-0.95, 1.05]上の一様分布(平均0.05、分散1/3:対立仮説が正しい)
・一様分布C:[-0.9, 1.1]上の一様分布(平均0.1、分散1/3:対立仮説が正しい)
・一様分布D:[-0.8, 1.2]上の一様分布(平均0.2、分散1/3:対立仮説が正しい)
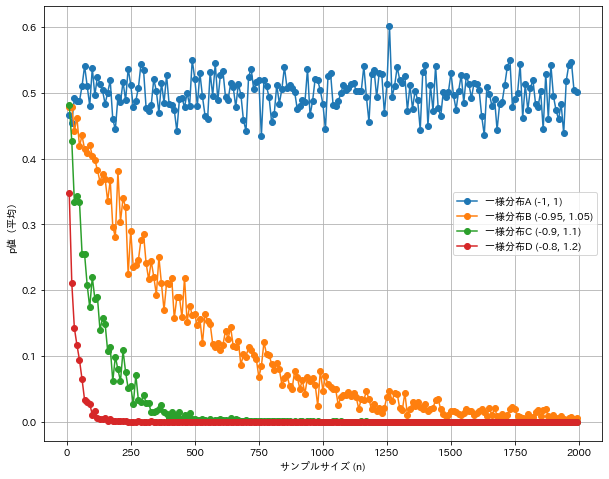
この結果から、以下の情報が読み取れそうです。
・実際に母平均が
・母平均が0でない一様分布では、母平均が0から離れるほどに
まとめ
この記事では、
(参考)実験に用いたコード
#import
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline
#function
def two_sided_test(distribution_func, params, known_variance, sample_size, num_experiments):
"""
両側検定のシミュレーション関数
distribution_func: 母集団の分布関数
params: 分布関数のパラメータ
known_variance: 既知の分散
sample_size: サンプル数
num_experiments: 実験回数
"""
p_values = []
for _ in range(num_experiments):
sample = distribution_func(*params, sample_size)
z_score = np.mean(sample) / (np.sqrt(known_variance) / np.sqrt(sample_size))
p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))
p_values.append(p_value)
return np.mean(p_values), p_values
#config
distributions = {
'一様分布A (-1, 1)': (np.random.uniform, (-1, 1)),
'一様分布B (-0.95, 1.05)': (np.random.uniform, (-0.95, 1.05)),
'一様分布C (-0.9, 1.1)': (np.random.uniform, (-0.9, 1.1)),
'一様分布D (-0.8, 1.2)': (np.random.uniform, (-0.8, 1.2)),
}
results = {}
sample_sizes = range(10, 2000, 10)
num_experiments = 100
known_variance = 1/3
#caculation
for dist_name, (dist_func, params) in distributions.items():
p_value_means = []
for n in sample_sizes:
mean_p_value, _ = two_sided_test(dist_func, params, known_variance, n, num_experiments)
p_value_means.append(mean_p_value)
results[dist_name] = p_value_means
#plot
plt.figure(figsize=(10, 8))
for dist_name, p_value_means in results.items():
plt.plot(sample_sizes, p_value_means, marker='o', linestyle='-', label=dist_name)
plt.xlabel('サンプルサイズ (n)')
plt.ylabel('p値(平均)')
plt.legend()
plt.grid(True)
plt.show()

 この記事をシェアする
この記事をシェアする





