はじめまして、 Customer Analytics Division / DX Technology Unit の渡邉です。普段は主に通信事業者の基地局設備のデータを扱う業務を行っています。今回は「傾向スコアの学習に入れてはいけない変数」について、ご紹介します。
サマリ
- ランダム化比較試験 (RCT:randomized controlled trial)が行えない場合、因果効果を得るために、傾向スコアを用いる手法が用いられることがあります。
- しかし、Judea Pearl流の構造方程式を用いた因果推論によれば、傾向スコアの学習に含めるとバイアスを生む変数の条件が示されていますが、あまりこの辺を注視されていないような気がしています。
- そこで、文献を調査し、バイアスを生む条件を理論的に示しました。その後、サンプルデータにおいても実験し、バイアスが存在することを確かめました。
理論編
Judea Pearlの因果推論について基礎をまとめます。
1.構造的因果モデル (SCM:Structural Causal Model)
因果には方向が存在していると考えられるでしょう。例えば、ある薬の投与が、病気からの回復に効果があるかどうか調べているとします。性別が、この効果に影響を及ぼすとしましょう。このとき、薬の投与が性別に影響を与えたり、病気からの回復が性別に影響を与えることは無いでしょう。この場合は、次のようなSCMが考えられます。ここで、投薬の有無をX、回復をY、性別をZとして
\(V=\{X, Y, Z\},U=\{U_X, U_Y,U_Z\}, F=\{f_1, f_2\}\)
\(X=f_1(Z, U_X) ,Y=f_2(X, Z, U_Y), Z=U_Z\)
と表すことができます。ここで、VはSCMに登場する変数集合、Uは各変数の誤差変数の集合とします。「投薬は、性別と観測できない影響によって決まる」「回復は、投薬と性別と観測できない影響によって決まる」ということを表しています。
2.因果グラフ
上述したSCMをグラフィカルに表現します。右辺から左辺に矢印を引くだけです。
改めて、「投薬は、性別と観測できない影響によって決まる」「回復は、投薬と性別と観測できない影響によって決まる」ということがグラフィカルに理解できます。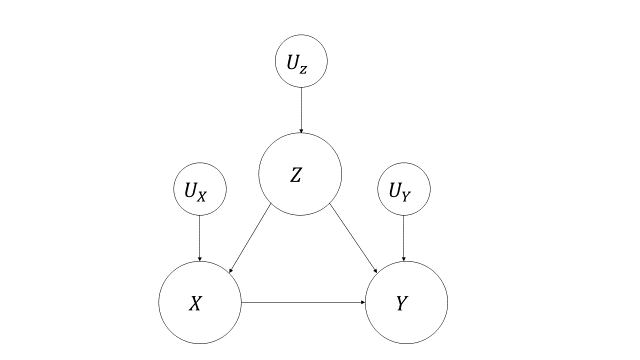
3.SCMに基づく介入の定義
ランダム化試験の何がうれしかったのかをおもいだしてみると、未観測の変数が介入変数に与える影響をなくすことができる点でした。このことを今回のSCMで表すと、例えば投薬をする場合は
\(V=\{X, Y, Z\},U=\{U_X, U_Y,U_Z\}, F=\{f_2\}\)
\(X=1 ,Y=f_2(X, Z, U_Y), Z=U_Z\)
と書き換えられることになります。投薬はもはや性別と観測できない変数の影響を受けていません。
介入後のSCMを因果グラフで表すと次のようになります。
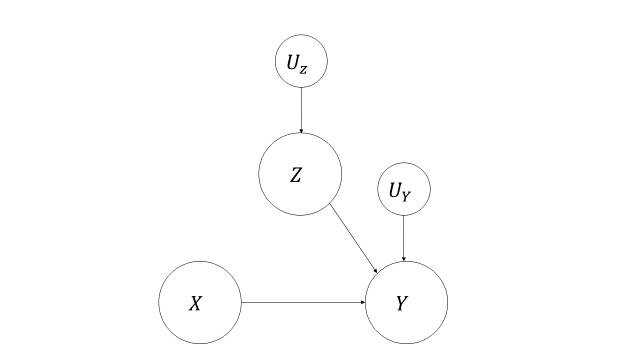
4.平均因果効果の導入
上で述べた介入の操作を代数的に表します。介入前のグラフに基づいた確率分布をPとして、
\(P(Y=y|do(X=x))\)
と表します。do演算子と呼びます。例えば、上記の例では「全員に薬を投与した場合、全員に薬を投与しなかった場合の回復する確率の差」が知りたい因果効果として妥当でしょう。これを平均因果効果(ACE : average causal effect)と呼ぶことにして、次の式で表します。
\(ACE=P(Y=1|do(X=1))-P(Y=1|do(X=0))\)
5.因果効果の推定
問題は、do演算子が含まれていると、その確率をデータから推定することができないことです。これを解決するために、介入後のグラフに基づいた確率分布\(P_m\)とおいて、\(P\)と\(P_m\)との共通点を探ってみると、以下に気が付きます。
\(P(Z=z)\)は介入前後で変化しない
条件付き確率\(P(Y=y|Z=z, X=x)\)は介入前後で変化しない
よって次の式変形が成り立ち、データから因果効果を推定できることがわかります。
\(P(Y=y|do(X=x))\)
\(=P_m(Y=y|X=x)\) (定義による)
\(=\sum_z P_m(Y=y|X=x, Z=z)P_m(Z=z|X=x)\)
\(=\sum_z P_m(Y=y|X=x, Z=z)P_m(Z=z)\) (今回のSCMによる)
\(=\sum_z P(Y=y|X=x, Z=z)P(Z=z)\) (上記で挙げた\(P\)と\(P_m\)との共通点による)
このとき、「変数Zで調整する」という言葉遣いをします。
上記を一般化すると、介入変数のすべての親で調整を行うとACEが推定できることが知られています。次の定理としてまとめます。
グラフ\(G\)において、\(X\)の親を \(PA\)とすると、\(X\)が\(Y\)に及ぼす因果効果は
\(P(Y=y|do(X=x))=\sum_z P(Y=y|X=x, PA=z)P(PA=z)\)
で与えられる。
6.調整してはいけない変数
上で述べた基準は、バイアスなくACEを推定するために必要な変数集合を与えてくれるものでした。必要な変数集合だけでなく、余計な変数も調整するとどうなるでしょうか。
つまり、上記定理において、Xの親だけでなく他の変数も調整してしまったらどうなるでしょうか。
実は、調整するとバイアスを生む変数のタイプが知られています。
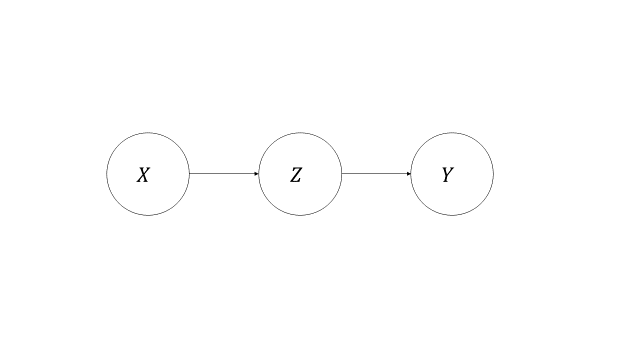
中間変数
介入変数から目的変数に伸びる矢印の途中にある変数
例:次の図のZ
コライダー
介入変数からその変数に矢印が伸びていて、目的変数からその変数に矢印が伸びている
例:次の図のZ
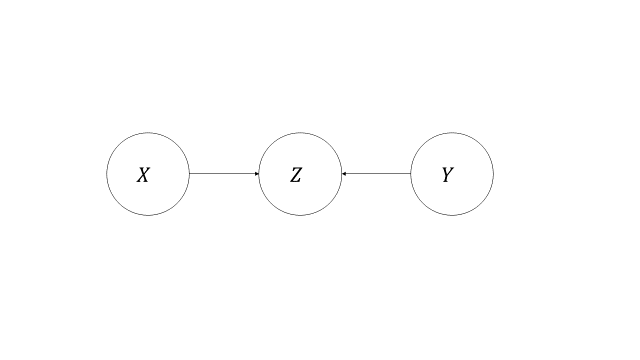
7.共変量同値と傾向スコア
傾向スコアで調整することは、それを推定するために学習した変数すべてで調整することと同値であることが知られています。
共変量同値という定理から導かれます。
8.今回の本題
やっと本題です。。。
次の2点を述べました。
・「因果効果を推定するためには介入変数のすべての親を含めて調整をしなければならない。その際、中間変数やコライダーを含めるとバイアスを生む。」
・「傾向スコアで調整することは、それを推定するために学習した変数のすべてで調整することと同値である。」
∟このことから、「傾向スコアマッチングをするとき、傾向スコアの学習に中間変数やコライダーを含めるとバイアスを生んでしまう。」ということが導かれます。実際にどうなるか確かめるため、実験を行いました。
実践編
サマリ
・因果効果が0.095であるデータセットを作成した。
∟今回は人工データセットであるため、介入変数のすべての親がわかります。
・介入変数のすべての親と傾向スコア学習に含み、傾向スコアマッチングを行ったところ因果効果が0.0067と推定された。
∟明らかに過小推定。
・介入変数のすべての親を傾向スコア学習に含み、傾向スコアマッチングを行ったところ因果効果が0.081と推定された。
∟多少過小推定だが、上と比較すればかなり真の因果効果に近い。
∟中間変数を傾向スコアの学習に含まない方がいいということが分かった!
ノートブック
・人工のデータを作成し、それに対して傾向スコアマッチングを行い因果効果を推定しています。
・データの設定としては、あるホテルにおいて、予約と異なる部屋を割り当ててしまうことが予約のキャンセルを発生させるメカニズムをイメージしています。
∟Booking Cancelled:その予約がキャンセルされたか(目的変数)
∟Different Room Assigned:予約と異なる部屋を割り当てたかどうか(介入変数)
∟is_claimed:クレームが行われたかどうか(中間変数)
∟Booking Changes:顧客が予約を変更したか
∟hotel:ホテルの種類
・実行したノートブックはこちらです!
まとめと因果推論を行う際の示唆
・傾向スコアの学習に中間変数を含むと、含まない場合より、因果効果の推定誤差が大きくなりました。
∟理論編で確認したことにより、中間変数でなくコライダーでも同様の結果にあるはずです。
∟また、傾向スコアの学習のみならず、MetaLeaner系でも同様の結果になるはずです。
・よって、因果構造を正しく捉えられているかどうかが重要であることが示唆されます。
・ビジネスのメカニズムに対し深い洞察を持つことは、因果推論を行う際の何よりも重要な要素なのではないでしょうか。
参考文献
理論編における参考にした文献を紹介します。
1,2,3:「入門統計的因果推論」,Judea Pearl (著), Madelyn Glymour (著), Nicholas P. Jewell (著), 落海 浩 (翻訳),朝倉書店,2019, 1章
4,5:「入門統計的因果推論」,3章
6: 中間変数について
「因果推論の科学 「なぜ?」の問いにどう答えるか」 ,ジューディア・パール (著), ダナ・マッケンジー (著), 松尾 豊 (解説), 夏目 大 (翻訳),文藝春秋,2022,p237
「統計的因果推論の理論と実装」 ,高橋 将宜(著),共立出版,2022,p104
コライダーについて
「因果推論の科学 「なぜ?」の問いにどう答えるか」, p246, p282
7:「構造的因果モデルの基礎」 ,黒木 学 (著),共立出版,2017,p104




