初めまして。Social Innovation Divisionの木本と申します。 普段の業務では、ヘルスケアアプリで収集されるデータの分析を行っています。
本記事では生存時間分析について概要を説明した後、通信会社の顧客離脱に関するサンプルデータを用いたマーケティング分野での活用例を紹介します。
生存時間分析とは
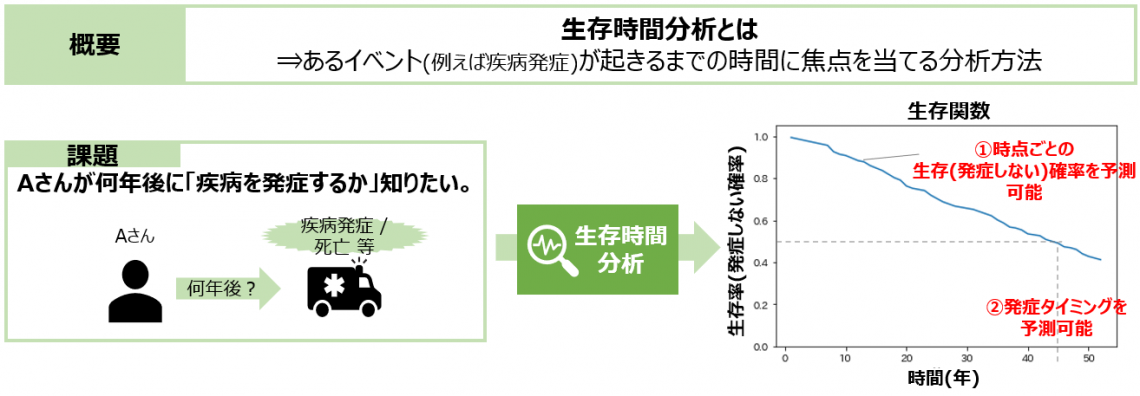
あるイベント(例えば疾病発症)が起きるまでの時間に焦点を当てる分析方法を生存時間分析といいます。
例えばAさんが何年後に「疾病を発症するか」知りたいとします。生存時間分析を行うと、Aさんについて、①生存関数と呼ばれる時点ごとの生存確率の予測値が取得できます。また、②生存確率に対する発症タイミングを予測することができます。
生存時間分析の流れ
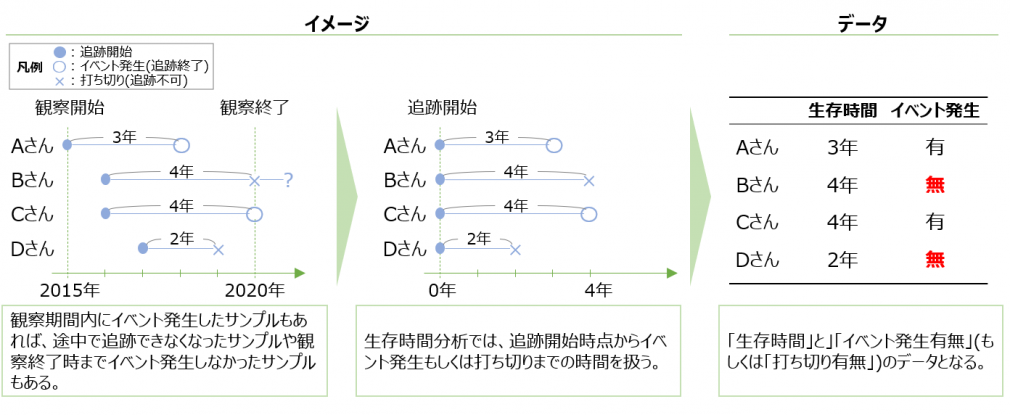
あるデータに対して生存時間分析を用いる場合、生存期間とイベント発生有無について整理する必要が出てきます。 ここでイベント発生無しと定義したデータを打ち切り(※)と呼び、対象にイベントが起こらずに観察期間が終了した場合やなんらかの理由で対象を観察できなくなってしまったなど、生存時間が正確にわからない場合のイベント定義を指します。
※正確には、不完全な観測値には打ち切りと切断の2つのメカニズムが存在しますが、この記事では取り扱いません。
一般的なモデルとの違い
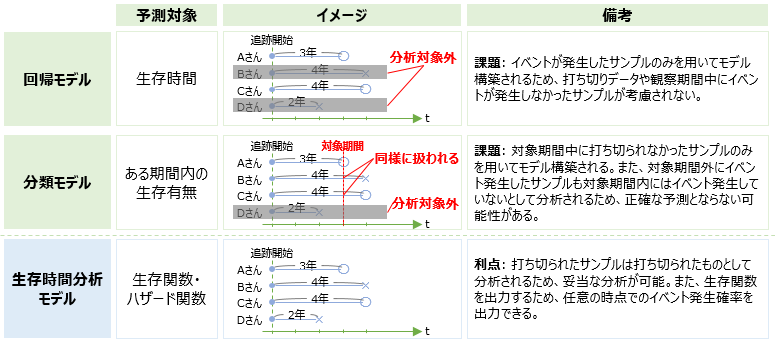
通常、観測データには、打ち切りデータが存在します。
一般的な回帰モデルや分類モデルでは打ち切りデータを扱うことができないため、分析対象から除外することになりますが、生存時間分析のモデルは打ち切りデータを扱えるという特徴があります。これにより、特に打ち切りデータが多いデータに対しては、妥当な分析ができると考えられます。
生存時間分析の適用例
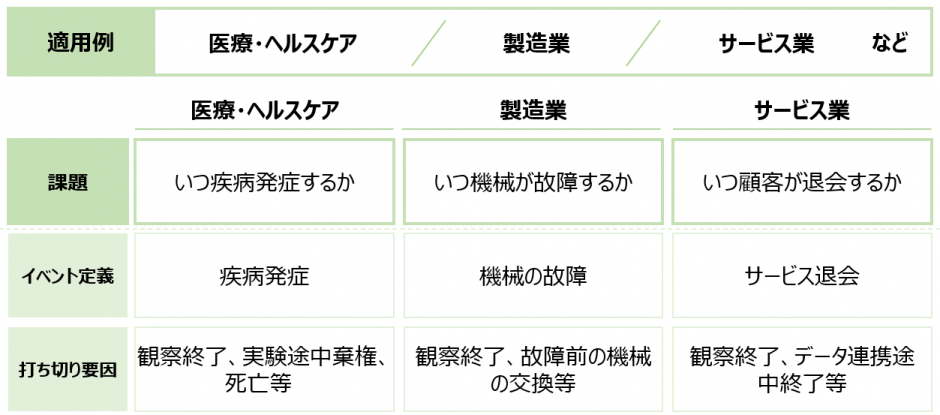
生存時間というと、医療・ヘルスケアに限った分析手法として見られがちですが、イベントの定義を工場の機械の故障やECサイトにおけるサービスの退会とすると、製造業やサービス業においても有用なモデリング手法として用いることができます。
生存時間分析で用いられるモデル
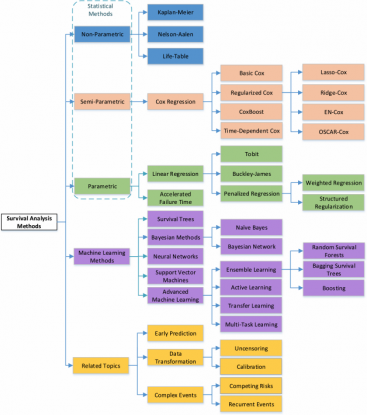
Ping Wang et al. (2019)
上記は生存時間分析に関するサーベイ論文[1]で述べられている生存時間分析の分類になります。
生存時間分析で用いられるモデルとしては、大きく以下の4つに大別されます。
- ノンパラメトリック
- セミパラメトリック
- パラメトリック
- 機械学習
これらのモデルでは生存時間の確率変数Tを用いて以下で定義されるハザード関数を導入します。
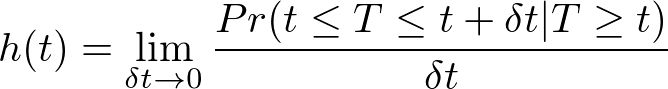
定義からわかるように、これはある時点tまで生存したという条件のもとで、微小時間内に死亡する確率のようなものと捉えることができます。
セミパラメトリックモデルのCox比例ハザードモデルは最もよく用いられており、多くの医学系論文では本手法を用いて生存時間の推定が行われています。Cox比例ハザードモデルでは、このハザード関数を以下のように定式化した上でモデルのフィッティングを行います(x_1, x_2…x_pは説明変数)。 βは部分尤度の最大化により推定されます(最尤推定)。
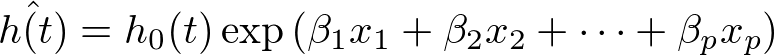
このモデルは、ハザード比(≒リスク比)が時間によらず一定であるという重要な特徴を持っています。この特徴を比例ハザード性と呼びます。
例として x_1=𝑎 と 𝑥_1=𝑏 のハザード比を考えると、
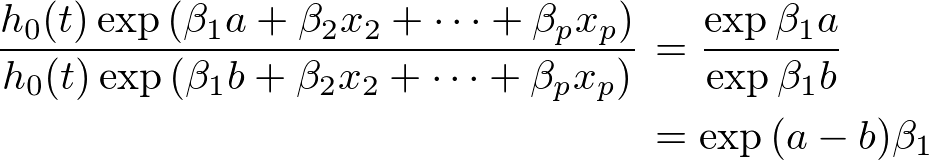
この特徴のお陰で、Cox比例ハザードモデルを用いてモデリングを行うと、ある共変量が異なった場合のリスク比が定量化できるようになり解釈が容易となります。
顧客離脱を対象とした生存時間分析
最後に、弊社らしく通信会社のデータを用いて生存時間分析で示唆を出してみましょう。
サンプルデータについて
サンプルデータとして、今回はKaggleで公開されているTelco Customer Churn[2]を用います。 各行は顧客を表し、各列にはメタデータ列に記述されている顧客の属性が含まれています。データセットには、以下の情報が含まれています。
- 顧客が各種サービスを契約したか否か:電話サービス、複数回線、インターネット、オンラインセキュリティ、オンラインバックアップ、テクニカルサポート、テレビや映画のストリーミング等
- 顧客情報:顧客であった期間、契約、支払い方法、ペーパーレス決済、月額料金、および合計料金
- 基礎情報:性別、年齢層、およびパートナーと扶養家族がいるかどうか
Cox比例ハザードモデルを用いたモデリング
Pythonでは、lifelinesというパッケージを用いると、生存時間分析を簡単に実装することができます。以下で使用しているinput_dfは、上述した公開データを整形して作成しました(ダミー化及び欠損除去)。
# lifelinesをインポート
import lifelines
# lifelinesパッケージからCox比例ハザードモデルを使用
cph = lifelines.CoxPHFitter()
# duration_colに生存時間の列を、event_colにイベントの列を指定
cph.fit(input_df, duration_col='tenure', event_col='Churn', show_progress=False)
# 回帰係数、Zスコア、p-value等をまとめた表を表示
cph.print_summary()
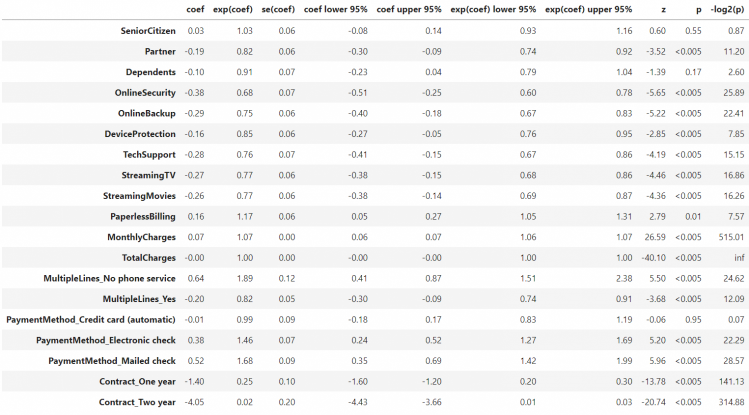
結果では、exp(coef)に着目します。
モデルの定義から、これが1を超えると、その説明変数が高くなった場合にイベント発症確率を高くする方向に寄与、1よりも低いとその説明変数が高くなった場合にイベント発症確率を低くする方向にその共変量が寄与していると考えることができます。
例えば Partner(パートナー有無)のexp(coef)は0.82となっています。ここから、パートナーがいる場合(Partner=1)の解約のしやすさはパートナーがいない場合(Partner=0)と比較して0.82倍となっており、パートナーがいる方がやや解約しにくいことがわかります。
Forest Plotの描画
上述したような係数の解釈を視覚的に行うため、各変数の係数とその信頼区間を高い順にプロットします。このプロットをForest Plotと呼びます。
# 係数とその信頼区間を描画
fig_coef, ax_coef = plt.subplots(figsize=(12,7))
ax_coef.set_title('Forest Plot')
cph.plot(ax=ax_coef)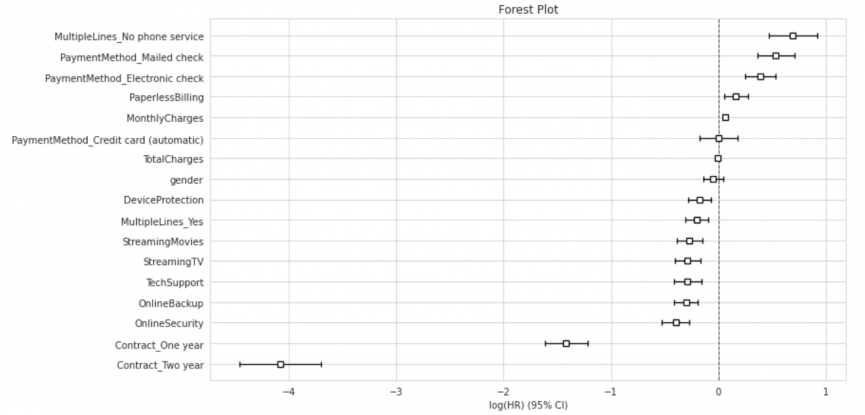
契約形態ごとに生存関数を描画
Contract変数は契約形態を表しており、月ごと契約(Month to Month)、1か年契約(One year)、2か年契約(Two year)の3種類存在します。
今回のデータではContract変数をエンコーディングしたContract_One year、Contract_Two yearというダミー変数に変換されています。
Contract_One year、Contract_Two yearの値から、解約率抑止に最も寄与している Contract(契約形態)変数について、他のすべての変数を一定としながら単一の共変量を変化させた場合の生存曲線を描画します。
cph.plot_partial_effects_on_outcome(['Contract_One year', 'Contract_Two year', ], values=np.eye(2)) 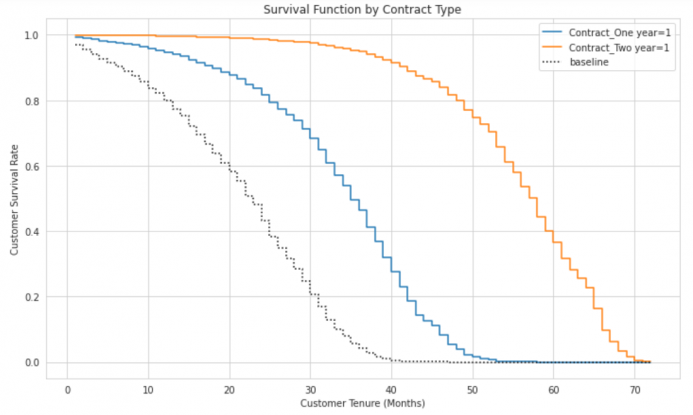
生存関数を40か月経過後で比較すると、月毎契約(ベースライン)の人の継続確率はほぼ0%となっているのに対し、1か年契約の人は30%程度、2か年契約の人は約90%程度となる推定がされていることがわかります。
その他の変数についても同様に見ていくことで、その影響度を可視化し示唆につなげることができます。
終わりに
今回は単純なCox比例ハザードモデルを例に、分析例を見ていきましたが、 最近では、Random Survival Forests[3]やDeep Surv[4]といった生存時間分析に機械学習を適用している手法も現れてきています。イベント発生に関するデータがあれば、是非一度利用を検討してみて下さい。
参考文献
[1] Ping Wang, Yan Li, and Chandan K. Reddy. 2019. Machine Learning for Survival Analysis: A Survey. ACM Comput. Surv. 51, 6, Article 110 (February 2019), 36 pages. DOI:https://doi.org/10.1145/3214306
[2] https://www.kaggle.com/blastchar/telco-customer-churn
[3] https://arxiv.org/pdf/0811.1645.pdf
[4] Katzman, J.L., Shaham, U., Cloninger, A. et al. DeepSurv: personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med Res Methodol 18, 24 (2018). https://doi.org/10.1186/s12874-018-0482-1




